پروفسور جي ان ردي يك استاد برجسته در دانشكده مهندسي مكانيك دانشگاه تگزاس مي باشد. اين استاد برجسته در سطح بين المللي به خاطر تبحر در علوم مكانيك محاسباتي و مكانيك كاربردي و همچنين تاليف 17 كتاب و ارائه بيش از 450 مقاله در ژورنال هاي مختلف علمي شناخته شده مي باشد. كتاب مقدمه اي بر مكانيك محيط هاي پيوسته پروفسور ردي فرم غيرمادي و جزء را معرفي مي نمايد. در اين كتاب فرم معادلات اساسي و برنامه هاي كاربردي آنها به مشكلات در كشش، مكانيك سيالات، و انتقال حرارت و معرفي مختصر به ويسكوالاستيك خطي را نيز ارائه مي دهد. اين كتاب براي دانشجويان تحصيلات تكميلي بسيار ايده آل مي باشد. همچنين اين كتاب براي كساني كه به دنبال كار بيشتر در زمينه هاي ديناميك سيالات، انعطاف پذيري، صفحات و پوسته ها، ويسكوزولاسيون، پلاستيك و زمينه هاي بين رشته اي مانند ژئومكانيك، بيومكانيك، مكانيولوژي و علوم نانو هستند مي تواند مفيد واقع گردد...
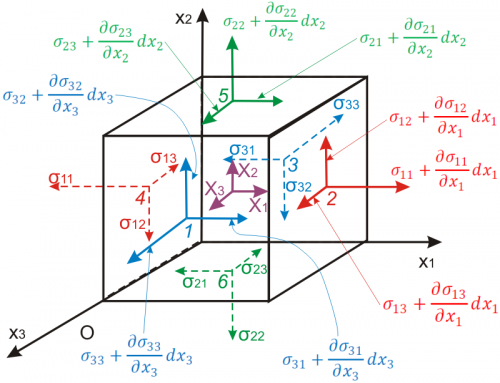
كتاب مقدمه اي بر مكانيك محيط هاي پيوسته (Introduction to Continuum Mechanics)، مشتمل بر 480 صفحه، در 9 فصل، با فرمت PDF، به زبان انگليسي، همراه با مثال ها و تمرينات متعدد به ترتيب زير گردآوري شده است:
Chapter 1: Introduction
- Continuum Mechanics
- A Look Forward
- Summary
- Problems
Chapter 2: VECTORS AND TENSORS
- Background and Overview
- Vector Algebra
- Definition of a Vector
- Vector addition
- Multiplication of a vector by a scalar
- Linear independence of vectors
- Scalar and Vector Products
- Scalar product
- Vector product
- Triple products of vectors
- Plane Area as a Vector
- Reciprocal Basis
- Components of a vector
- General basis
- Ortho normal basis
- The Gram–Schmidt ortho normalization
- Summation Convention
- Dummy index
- Free index
- Kronecker delta
- Permutation symbol
- Transformation Law for Different Bases
- General transformation laws
- Transformation laws for orthonormal systems
- Theory of Matrices
- Definition
- Matrix Addition and Multiplication of a Matrix by a Scalar
- Matrix Transpose
- Symmetric and Skew Symmetric Matrices
- Matrix Multiplication
- Inverse and Determinant of a Matrix
- Positive-Definite and Orthogonal Matrices
- Vector Calculus
- Differentiation of a Vector with Respect to a Scalar
- .Curvilinear Coordinates
- The Fundamental Metric
- Derivative of a Scalar Function of aVector
- The Del Operator
- Divergence and Curl of a Vector
- Cylindrical and Spherical Coordinate Systems
- Gradient, Divergence, and Curl Theorems
- Tensors
- Dyads and Dyadics
- Nonion Form of a Second-Order Tensor
- Transformation of Components of a Tensor
- Higher-Order Tensors
- Tensor Calculus
- Eigenvalues and Eigenvectors
- Eigenvalue problem
- Eigenvalues and eigen vectors of a real symmetric tensor
- Spectral theorem
- Calculation of eigenvalues and eigen vectors
- Summary
- Problems
Chapter 3: KINEMATICS OF CONTINUA
- Introduction
- Descriptions of Motion
- Configurations of a Continuous Medium
- Material Description
- Spatial Description
- Displacement Field
- Analysis of Deformation
- Deformation Gradient
- Isochoric, Homogeneous, and In homogeneous Deformation
- Isochoric deformation
- Homogeneous deformation
- Nonhomogeneous deformation
- Change of Volume and Surface
- Volume change
- Area change
- Strain Measures
- Cauchy Green Deformation Tensors
- Green Lagrange Strain Tensor
- Physical Interpretation of Green–Lagrange Strain Components
- Cauchy and Euler Strain Tensors
- Transformation of Strain Components
- Invariants and Principal Values of Strains
- Infinitesimal Strain Tensor and Rotation Tensor
- Infinitesimal Strain Tensor
- Physical Interpretation of Infinitesimal Strain
- Tensor Components
- Infinitesimal Rotation Tensor
- Infinitesimal Strains in Cylindrical and Spherical
- Coordinate Systems
- Cylindrical coordinate system
- Spherical coordinate system
- Velocity Gradient and Vorticity Tensors
- Relationship Between D and ˙E
- Compatibility Equations
- Preliminary Comments
- Infinitesimal Strains
- Finite Strains
- Rigid-Body Motions and Material Objectivity
- Superposed Rigid-Body Motions
- Introduction and rigid-body transformation
- Effect on F
- Effect on C and E
- Effect on L and D
- Material Objectivity
- Observer transformation
- Objectivity of various kinematic measures
- Time rate of change in a rotating frame of reference
- Polar Decomposition Theorem
- Preliminary Comments
- Rotation and Stretch Tensors
- Objectivity of Stretch Tensors
- Summary
- Problems
Chapter 4: STRESS MEASURES
- Introduction
- Cauchy Stress Tensor and Cauchy’s Formula
- Stress Vector
- Cauchy’s Formula
- Cauchy Stress Tensor
- Transformation of Stress Components and Principal Stresses
- Transformation of Stress Components
- Invariants
- Transformation equations
- Principal Stresses and Principal Planes
- Maximum Shear Stress
- Other Stress Measures
- Preliminary Comments
- First Piola ******chhoff Stress Tensor
- Second Piola ******chhoff Stress Tensor
- Equilibrium Equations for Small Deformations
- Objectivity of Stress Tensors
- Cauchy Stress Tensor
- First Piola ******chhoff Stress Tensor
- Second Piola ******chhoff Stress Tensor
- Summary
- Problems
Chapter 5: CONSERVATION AND BALANCE LAWS
- Introduction
- Conservation of Mass
- Preliminary Discussion
- Material Time Derivative
- Vector and Integral Identities
- Vector identities
- Integral identities
- Continuity Equation in the Spatial Description
- Continuity Equation in the Material Description
- Reynolds Transport Theorem
- Balance of Linear and Angular Momentum
- Principle of Balance of Linear Momentum
- Equations of motion in the spatial description
- Equations of motion in the material description
- Spatial Equations of Motion in Cylindrical and Spherical Coordinates
- Cylindrical coordinates
- Spherical coordinates
- Principle of Balance of Angular Momentum
- Mono polar case
- Multi polar case
- Thermodynamic Principles
- Balance of Energy
- Energy equation in the spatial description
- Energy equation in the material description
- Entropy Inequality
- Homogeneous processes
- In homogeneous processes
- Conservation and Balance Equations in the Spatial Description
- Conservation and Balance Equations in the Material Description
- Closing Comments
- Problems
Chapter 6: CONSTITUTIVE EQUATIONS
- Introduction
- General Comments
- General Principles of Constitutive Theory
- Material Frame Indifference
- Restrictions Placed by the Entropy Inequality
- Elastic Materials
- Cauchy Elastic Materials
- Green-Elastic or Hyper elastic Materials
- Linearized Hyper elastic Materials: Infinitesimal Strains
- Hookean Solids
- Generalized Hooke’s Law
- Material Symmetry Planes
- Monoclinic Materials
- Orthotropic Materials
- Isotropic Materials
- Nonlinear Elastic Constitutive Relations
- Newtonian Fluids
- Ideal Fluids
- Viscous In compressible Fluids
- Generalized Newtonian Fluids
- Inelastic Fluids
- Power law model
- Carreau model
- Bingham model
- Visco elastic Constitutive Models
- Differential models
- Integral models
- Heat Transfer
- Fourier’s Heat Conduction Law
- Newton’s Law of Cooling
- Stefan–Boltzmann Law
- Constitutive Relations for Coupled Problems
- Electro magnetics
- Maxwell’s equations
- Constitutive relations
- Thermo elasticity
- Hygro thermal elasticity
- Electro elasticity
- Summary
- Problems
Chapter 7: LINEARIZED ELASTICITY
- Introduction
- Governing Equations
- Preliminary Comments
- Summary of Equations
- Strain displacement equations
- Equations of motion
- Constitutive equations
- Boundary conditions
- Compatibility conditions
- The Navier Equations
- The Beltrami Michell Equations
- Solution Methods
- Types of Problems
- Types of Solution Methods
- Examples of the Semi Inverse Method
- Stretching and Bending of Beams
- Superposition Principle
- Uniqueness of Solutions
- Clapeyron’s, Betti’s, and Maxwell’s Theorems
- Clapeyron’s Theorem
- Betti’s Reciprocity Theorem
- Maxwell’s Reciprocity Theorem
- Solution of Two-Dimensional Problems
- Plane Strain Problems
- Plane Stress Problems
- Unification of Plane Stress and Plane Strain Problems
- Airy Stress Function
- Saint Venant’s Principle
- Torsion of Cylindrical Members
- Warping function
- Prandtl’s stress function
- Methods Based on Total Potential Energy
- The Variational Operator
- The Principle of the Minimum Total Potential Energy
- Construction of the total potential energy functional
- Euler’s equations and natural boundary conditions
- Minimum property of the total potential energy functional
- Castigliano’s TheoremI
- The Ritz Method
- The variational problem
- Description of the method
- Hamilton’s Principle
- Hamilton’s Principle for a Rigid Body
- Hamilton’s Principle for a Continuum
- Summary
- Problems
Chapter 8: FLUID MECHANICS AND HEAT TRANSFER
- Governing Equations
- Preliminary Comments
- Summary of Equations
- Fluid Mechanics Problems
- Governing Equations of Viscous Fluids
- In viscid Fluid Statics
- Parallel Flow (Navier Stokes Equations)
- Problems with Negligible Convective Terms
- Energy Equation for One-Dimensional Flows
- Heat Transfer Problems
- Governing Equations
- Heat Conduction in a Cooling Fin
- Axisymmetric Heat Conduction in a Circular Cylinder
- Two Dimensional Heat Transfer
- Coupled Fluid Flow and Heat Transfer
- Summary
- Problems
Chapter 9: LINEARIZED VISCOELASTICITY
- Introduction
- Preliminary Comments
- Initial Value Problem, the Unit Impulse, and the Unit Step Function
- The Laplace Transform Method
- Spring and Dashpot Models
- Creep Compliance and Relaxation Modulus
- Maxwell Element
- Creep response
- Relaxation response
- Kelvin Voigt Element
- Creep response
- Relaxation response
- Three Element Models
- Four Element Models
- Integral Constitutive Equations
- Hereditary Integrals
- Hereditary Integrals for Deviatoric Components
- The Correspondence Principle
- Elastic and Viscoelastic Analogies
- Summary
- Problems

جهت دانلود كتاب مقدمه اي بر مكانيك محيط هاي پيوسته (Introduction to Continuum Mechanics)، برلينك زير كليك نماييد.
 روش هاي اجزاي محدود
روش هاي اجزاي محدود آموزش مقدماتي تا پيشرفته روش هاي عناصر محدود غير خطي
آموزش مقدماتي تا پيشرفته روش هاي عناصر محدود غير خطي مجموعه آموزش روش هاي اجزاي محدود مقدماتي
مجموعه آموزش روش هاي اجزاي محدود مقدماتي روش اجزاي محدود مقدماتي
روش اجزاي محدود مقدماتي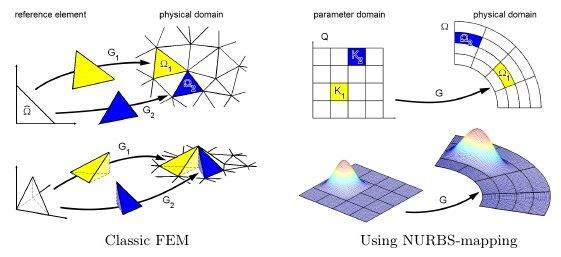 برنامه المان چهار گرهي تنش مسطح و كرنش مسطح در نرم افزار MATLAB
برنامه المان چهار گرهي تنش مسطح و كرنش مسطح در نرم افزار MATLAB طراحي قالب تزريق پلاستيك (Injection Mold Design)
طراحي قالب تزريق پلاستيك (Injection Mold Design)